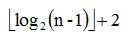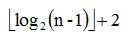写在前面 因为之前4月份打了将近一个月的个人赛,有些以前学习过的算法已经忘了,所以重新再温习一遍。
关于线段树 这里提一下完全二叉树。完全二叉树是叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。若设二叉树的深度为h,除第h层外,其它各层(1~h-1)的结点数都达到最大个数,第h层所有的结点都连续集中在最左边。那么线段树就是完全二叉树,一定条件下成为满二叉树。线段树的主要思想是二分,也就是通过二分的方法来查找节点。假设有编号从1到n的n个点,每个点都存了一些信息,用[L,R]表示下标从L到R的这些点。线段树的用处就是,对编号连续的一些点进行修改或者统计操作,修改和统计的复杂度都是O(log2(n))。
线段树的原理,就是,将[1,n]分解成若干特定的子区间(数量不超过4*n),然后,将每个区间[L,R]都分解为少量特定的子区间,通过对这些少量子区间的修改或者统计,来实现快速对[L,R]的修改或者统计。由此看出,用线段树统计的东西,必须符合区间加法,否则,不可能通过分成的子区间来得到[L,R]的统计结果。
符合区间加法的例子:
数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
最大公因数(GCD)——总GCD = gcd(左区间GCD,右区间GCD)
最大值——总最大值=max(左区间最大值,右区间最大值)
不符合区间加法的例子:
一个问题,只要能化成对一些连续点的修改和统计问题,基本就可以用线段树来解决。
线段树的原理 (注:由于线段树的每个节点代表一个区间,以下叙述中不区分节点和区间,只是根据语境需要,选择合适的词)
线段树本质上是维护下标为1,2,..,n的n个按顺序排列的数的信息,所以,其实是“点树”,是维护n的点的信息,至于每个点的数据的含义可以有很多,
线段树是将每个区间[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 这里的除法是整数除法,即对结果下取整)直到 L==R 为止。
开始时是区间[1,n] ,通过递归来逐步分解,假设根的高度为1的话,树的最大高度为
线段树对于每个n的分解是唯一的,所以n相同的线段树结构相同,这也是实现可持久化线段树的基础。
下图展示了区间[1,13]的分解过程:
上图中,每个区间都是一个节点,每个节点存自己对应的区间的统计信息。
线段树的点修改 假设要修改[5]的值,可以发现,每层只有一个节点包含[5],所以修改了[5]之后,只需要每层更新一个节点就可以线段树每个节点的信息都是正确的,所以修改次数的最大值为层数
复杂度O(log2(n))
线段树的区间修改 在写线段树的区间修改的时候,我们需要先掌握一个知识点,就是懒惰标记。
什么是懒惰标记?
试想,我们在操作的时候有可能有这样的操作。首先进行区间修改,修改了800次,然后再进行一次查询。这样,如果我们每次都将整个线段树的数据进行更新,实际上是非常慢的,如果我们能用一段空间,来记录修改数据,只有在使用的时候,一次性更新,就非常的方便。
所以这也是懒惰标记的作用。可以先对修改的数据进行储存,只有在使用的时候才更新线段树。那么,理论上我们应该建一个跟线段树同样大小的数组,称为懒惰数组,表示了每个节点的懒惰标记。有这样的操作:
总之,就是不使用的时候就一直在积累,在使用的时候再统一更新。
那么懒惰数组的更新非常简单,对线段树更新的时候就可以添加到懒惰标记,但是在使用的时候,我们需要用一个函数来完成懒惰标记的下推操作,也就是更新积累的值。代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void Pushdown(int rt, int l, int r) //下推标记的函数。l,r为左子树,右子树的数字数量 { if (lz[rt]) { //下推标记 lz[rt << 1] += lz[rt]; lz[rt << 1 | 1] += lz[rt]; //修改子节点的Sum使之与对应的lz相对应 //int mid=(l+r)>>1;与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1] += lz[rt] * l; //Sum[rt<<1]+=(mid-l+1)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1 | 1] += lz[rt] * r; //Sum[rt<<1|1]+=(r-mid)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 //清除本节点标记 lz[rt] = 0; } }
lz数组,即lazy,就是懒惰标记数组。可以看出,当lz[rt]存在值的时候,就说明现在我在使用这个节点,而这个节点以及其下的节点需要更新了,所以就利用二叉树的性质向下传递更新数据,同时更新线段树中的数据。最终,要将该节点的懒惰标记清零。
注意,下推的时候不是一直更新到叶子节点,而是只更新当前节点以及2个子树,因为实际操作的时候,只要碰到对某节点的操作就要调用Pushdown()函数,所以每次只用下推一层即可。
Pushdown()函数的使用需要在下面的区间操作中添加。
区间修改:
单点更新类似二分查找,更新的时候对经过的路径进行操作就可以了。但是区间更新需要考虑整个区间。线段树除了叶子节点,都表示了一段区间的值,那么就要配合懒惰标记在整个区间上进行操作。
线段树的区间查询 区间查询的原理跟区间更新基本一样,也是看结点表示的数据范围有不同的操作。同样,在到某个结点的时候一定要调用Pushdown()。不同点在于跟数据操作无关,但是需要一个sum来储存收集到的区间数据,同时最后return。这样在递归完成以后最后返回的就是区间和了。理解区间修改后,区间查询就容易的多了。
线段树的储存结构 线段树是用数组来模拟树形结构,对于每一个节点R ,左子节点为 2 R (一般写作R<<1)右子节点为 2 R+1(一般写作R<<1|1)
然后以1为根节点,所以,整体的统计信息是存在节点1中的。
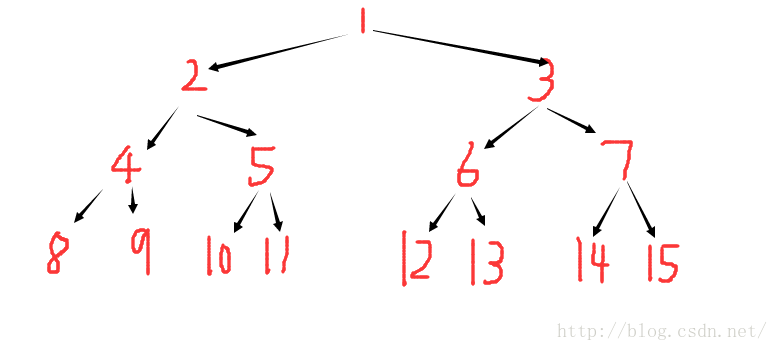
这么表示的原因看下图就很明白了,左子树的节点标号都是根节点的两倍,右子树的节点标号都是左子树+1:
线段树需要的数组元素个数很大,一般都开4倍空间,比如: int Sum[maxx<<2];
脱离lazy数组 lazy数组的使用在很大程度将降低了解决问题所耗费的时间,但是也增加了对模板的修改难度。诚然,lazy很实用,但是在一些问题的构造上并不容易修改。我们平常的区间修改,整个区间的数值变化是统一的,所以我们能够在数学上提前好多个结点先算出来更改情况。但是有很多问题并不是这样的。
例如:hdu4027。11年上海网络赛,要求区间内对每个节点的数值取其二次根。那么再考虑lazy数组就是徒生烦恼。如果我们抛弃lazy数组,直接每次都更新到叶子结点,同时考虑剪枝,速度也并不慢(500ms)。所以,在区间操作不平衡,同时可以剪枝的情况下,完全可以抛弃lazy数组,从而修改为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 boolean cleck(int rt,int l,int r){ // 剪枝条件 } void Update_tree_interval(int rt, int l, int r, int L, int R) { if (L == R) { Sum[rt] = 1; // 更新方式 return; } int mid = (L + R) / 2; if (mid >= l && cleck(rt << 1,L,mid)) Update_tree_interval(rt << 1, l, r, L, mid); if (mid < r && cleck(rt << 1 | 1,mid+1,R)) Update_tree_interval(rt << 1 | 1, l, r, mid + 1, R); Pushup(rt); }
线段树实现代码 首先:定义 1 2 3 4 5 6 7 8 #include <bits/stdc++.h> typedef long long ll; const int maxx = 10010; const int inf = 0x3f3f3f3f; using namespace std; int A[maxx]; //存原数组数据下标[1,n] int Sum[maxx << 2]; //Sum求和 int lz[maxx << 2]; //lz为懒惰标记
初始化 1 2 3 4 void init()//初始化 { memset(Sum,0,sizeof(Sum)); }
建树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void Pushup(int rt) //Pushup函数更新节点 { Sum[rt] = Sum[rt << 1] + Sum[rt << 1 | 1]; } void Build_tree(int l, int r, int rt) //建树,l,r表示当前节点区间,rt表示当前节点编号 { if (l == r) //若到达叶节点 { Sum[rt] = A[l];//cin>>Sum[rt]; return; } int mid = (l + r) >> 1; Build_tree(l, mid, rt << 1); Build_tree(mid + 1, r, rt << 1 | 1); Pushup(rt); }
这样的建树,是一个递归的过程。l与r分别表示区间,结合上面的图,当l==r的时候说明递归已经遍历到叶子节点了,而这个节点rt也是二叉树的节点编号。对应了数组的下标。所以进行赋值。然后直接return进行回溯。那么在正常递归的时候,我们需要利用二叉树的性质,即对于rt编号的节点而言,左子树编号为rt<<1,右子树为rt<<1|1。同样,由于二分的性质,利用mid = (l+r)/2,就可以获取下一个子树的区间范围。
在回溯的时候,是从树的最下层开始向最上层回溯,那么同样利用二叉树的性质,我们可以轻松将子树的数据加到父节点上。这样,当函数完成的时候,我们就可以利用数组来构建了一个线段树。
懒惰标记,下推操作 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void Pushdown(int rt, int l, int r) //下推标记的函数。l,r为左子树,右子树的数字数量 { if (lz[rt]) { //下推标记 lz[rt << 1] += lz[rt]; lz[rt << 1 | 1] += lz[rt]; //修改子节点的Sum使之与对应的lz相对应 //int mid=(l+r)>>1;与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1] += lz[rt] * l; //Sum[rt<<1]+=(mid-l+1)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1 | 1] += lz[rt] * r; //Sum[rt<<1|1]+=(r-mid)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 //清除本节点标记 lz[rt] = 0; } }
单点修改 线段树并不必须要进行区间的操作,如果是对单点进行操作,完全可以用更快的方法来实现。而对于单点修改而言,其实相比区间修改的代码要简单很多(因为lazy数组的存在),所以能用针对单点的修改最好不要用区间修改。单点更新非常类似二分查找,通过递归找到更新点的位置,在回溯的时候更新所有节点的值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void Update_tree_point(int l, int r, int rt, int a, int b) //点修改,假设A[a]=b,l,r表示当前节点区间,rt表示当前节点编号,a为更新点,b为更新值 { if (l == r) //到叶节点,修改 { A[a] = b; Sum[rt] = b; return; } int mid = (l + r) >> 1; //根据条件判断往左子树调用还是往右 // Pushdown(rt,mid-l+1,r-mid); 若既有点更新又有区间更新,需要这句话 if (a <= mid) Update_tree_point(l, mid, rt << 1, a, b); else Update_tree_point(mid + 1, r, rt << 1 | 1, a, b); Pushup(rt); }
区间修改 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void Update_tree_interval(int L, int R, int l, int r, int rt, int b) //区间修改,假设A[L,R]=b,L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号,b为更新值 { if (L <= l && r <= R) //如果本区间完全在操作区间[L,R]以内 { Sum[rt] += b * (r - l + 1); lz[rt] += b; //增加lz标记,表示本区间的Sum正确,子区间的Sum仍需要根据lz的值来调整 return; } int mid = (l + r) >> 1; Pushdown(rt, mid - l + 1, r - mid); //Pushdown(rt,l,r);//下推标记 //这里判断左右子树跟[L,R]有无交集,有交集才递归 if (L <= mid) Update_tree_interval(L, R, l, mid, rt << 1, b); if (R > mid) Update_tree_interval(L, R, mid + 1, r, rt << 1 | 1, b); Pushup(rt); //更新本节点信息 }
区间查询 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ll Query_tree(int L, int R, int l, int r, int rt) //区间查询,L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 { if (L <= l && r <= R) { //在区间内,直接返回 return Sum[rt]; } int mid = (l + r) >> 1; //下推标记,否则Sum可能不正确 Pushdown(rt, mid - l + 1, r - mid); //Pushdown(rt,l,r); ll sum = 0; //累计答案 if (L <= mid) sum += Query_tree(L, R, l, mid, rt << 1); if (R > mid) sum += Query_tree(L, R, mid + 1, r, rt << 1 | 1); return sum; }
线段树模板 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 #include <bits/stdc++.h> typedef long long ll; const int maxx = 10010; const int inf = 0x3f3f3f3f; using namespace std; int A[maxx]; //存原数组数据下标[1,n] int Sum[maxx << 2]; //Sum求和 int lz[maxx << 2]; //lz为懒惰标记 void init()//初始化 { memset(Sum,0,sizeof(Sum)); } void Pushup(int rt) //Pushup函数更新节点 { Sum[rt] = Sum[rt << 1] + Sum[rt << 1 | 1]; } void Pushdown(int rt, int l, int r) //下推标记的函数。l,r为左子树,右子树的数字数量 { if (lz[rt]) { //下推标记 lz[rt << 1] += lz[rt]; lz[rt << 1 | 1] += lz[rt]; //修改子节点的Sum使之与对应的lz相对应 //int mid=(l+r)>>1;与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1] += lz[rt] * l; //Sum[rt<<1]+=(mid-l+1)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 Sum[rt << 1 | 1] += lz[rt] * r; //Sum[rt<<1|1]+=(r-mid)*lz[rt];与下面Update_tree_interval函数中Pushdown(rt,l,r)对应 //清除本节点标记 lz[rt] = 0; } } void Build_tree(int l, int r, int rt) //建树,l,r表示当前节点区间,rt表示当前节点编号 { if (l == r) //若到达叶节点 { Sum[rt] = A[l];//cin>>Sum[rt]; return; } int mid = (l + r) >> 1; Build_tree(l, mid, rt << 1); Build_tree(mid + 1, r, rt << 1 | 1); Pushup(rt); } void Update_tree_point(int l, int r, int rt, int a, int b) //点修改,假设A[a]=b,l,r表示当前节点区间,rt表示当前节点编号,a为更新点,b为更新值 { if (l == r) //到叶节点,修改 { A[a] = b; Sum[rt] = b; return; } int mid = (l + r) >> 1; //根据条件判断往左子树调用还是往右 // Pushdown(rt,mid-l+1,r-mid); 若既有点更新又有区间更新,需要这句话 if (a <= mid) Update_tree_point(l, mid, rt << 1, a, b); else Update_tree_point(mid + 1, r, rt << 1 | 1, a, b); Pushup(rt); } void Update_tree_interval(int L, int R, int l, int r, int rt, int b) //区间修改,假设A[L,R]=b,L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号,b为更新值 { if (L <= l && r <= R) //如果本区间完全在操作区间[L,R]以内 { Sum[rt] += b * (r - l + 1); lz[rt] += b; //增加lz标记,表示本区间的Sum正确,子区间的Sum仍需要根据lz的值来调整 return; } int mid = (l + r) >> 1; Pushdown(rt, mid - l + 1, r - mid); //Pushdown(rt,l,r);//下推标记 //这里判断左右子树跟[L,R]有无交集,有交集才递归 if (L <= mid) Update_tree_interval(L, R, l, mid, rt << 1, b); if (R > mid) Update_tree_interval(L, R, mid + 1, r, rt << 1 | 1, b); Pushup(rt); //更新本节点信息 } ll Query_tree(int L, int R, int l, int r, int rt) //区间查询,L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 { if (L <= l && r <= R) { //在区间内,直接返回 return Sum[rt]; } int mid = (l + r) >> 1; //下推标记,否则Sum可能不正确 Pushdown(rt, mid - l + 1, r - mid); //Pushdown(rt,l,r); ll sum = 0; //累计答案 if (L <= mid) sum += Query_tree(L, R, l, mid, rt << 1); if (R > mid) sum += Query_tree(L, R, mid + 1, r, rt << 1 | 1); return sum; }
例题:HDU-1166 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 #include <bits/stdc++.h> typedef long long ll; const int maxx = 50010; const int inf = 0x3f3f3f3f; using namespace std; int A[maxx]; //存原数组数据下标[1,n] int Sum[maxx << 2]; //Sum求和 int lz[maxx << 2]; //lz为懒惰标记 void Pushup(int rt) //Pushup函数更新节点 { Sum[rt] = Sum[rt << 1] + Sum[rt << 1 | 1]; } void Build_tree(int l, int r, int rt) //建树,l,r表示当前节点区间,rt表示当前节点编号 { if (l == r) //若到达叶节点 { Sum[rt] = A[l];// //cin>>Sum[rt]; return; } int mid = (l + r) >> 1; Build_tree(l, mid, rt << 1); Build_tree(mid + 1, r, rt << 1 | 1); Pushup(rt); } void Update_tree_point(int l, int r, int rt, int a, int b) //点修改,假设A[a]=b,l,r表示当前节点区间,rt表示当前节点编号,a为更新点,b为更新值 { if (l == r) //到叶节点,修改 { //A[a] = b; Sum[rt] += b; return; } int mid = (l + r) >> 1; //根据条件判断往左子树调用还是往右 if (a <= mid) Update_tree_point(l, mid, rt << 1, a, b); else Update_tree_point(mid + 1, r, rt << 1 | 1, a, b); Pushup(rt); } ll Query_tree(int L, int R, int l, int r, int rt) //区间查询,L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 { if (L <= l && r <= R) { //在区间内,直接返回 return Sum[rt]; } int mid = (l + r) >> 1; ll sum = 0; //累计答案 if (L <= mid) sum += Query_tree(L, R, l, mid, rt << 1); if (R > mid) sum += Query_tree(L, R, mid + 1, r, rt << 1 | 1); return sum; } int main() { int t; scanf("%d", &t); string s; int cnt = 0; while (t--) { ++cnt; printf("Case %d:\n", cnt); int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &A[i]); Build_tree(1, n, 1); int x, y; cin >> s; while (s != "End") { scanf("%d%d", &x, &y); if (s == "Query") { printf("%d\n", Query_tree(x, y, 1, n, 1)); } else if (s == "Add") { Update_tree_point(1, n, 1, x, y); } else if (s == "Sub") { Update_tree_point(1, n, 1, x, -y); } cin >> s; } } return 0; }
线段树应用:扫描线求矩形面积并 分析:
1.矩形比较多,坐标也很大,所以横坐标需要离散化(纵坐标不需要),熟悉离散化后这个步骤不难,所以这里不详细讲解了,不明白的还请百度。
2.重点:扫描线法:假想有一条扫描线,从左往右(从右往左),或者从下往上(从上往下)扫描过整个多边形(或者说畸形。。多个矩形叠加后的那个图形)。如果是竖直方向上扫描,则是离散化横坐标,如果是水平方向上扫描,则是离散化纵坐标。下面的分析都是离散化横坐标的,并且从下往上扫描的。
扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值-1,下边给他一个值1,我们用一个结构体来保存所有的上下边。
1 2 3 4 5 struct segment { double l,r,h; //l,r表示这条上下边的左右坐标,h是这条边所处的高度 int f; //所赋的值,1或-1 }
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上 (总区间就是整个多边形横跨的长度) ,这个投影对应的其实是个插入和删除线段操作。 还记得给他们赋的值1或-1吗,下边是1,扫描到下边的话相当于往总区间插入一条线段,上边-1,扫描到上边相当于在总区间删除一条线段 (如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增1,扫描到上边对应的那一段的值都要减1, 如果总区间某一段的值为0,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的, 可以自己思考一下)。
每扫描到一条上下边后并投影到总区间后,就判断总区间现在被覆盖的总长度,然后用下一条边的高度减去当前这条边的高度,乘上总区间被覆盖的长度,就能得到一块面积,并依此做下去,就能得到最后的面积
(这个过程其实一点都不难,只是看文字较难体会,建议纸上画图,一画即可明白,下面献上一图希望有帮助)
扫描线求矩形面积并的例题:POJ-1151 题目给了n个矩形,每个矩形给了左下角和右上角的坐标,矩形可能会重叠,求的是矩形最后的面积。因为变化范围比较大,我们要用到离散化,离散化就不说了,重点说一说扫描线的过程:
下面有个矩形
现在假设我们有一根线,从下往上开始扫描
如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,那么剩下了一个变量,那就是矩形的长一直在变化。
我们的线段树就是为了维护矩形的长,我们给每一个矩形的上下边进行标记,下面的边标记为1,上面的边标记为-1,每遇到一个矩形时,我们知道了标记为1的边,我们就加进来这一条矩形的长,等到扫描到-1时,证明这一条边需要删除,就删去,利用1和-1可以轻松的到这种状态。
还要注意这里的线段树指的并不是线段的一个端点,而指的是一个区间,所以我们要计算的时候r+1和r-1
再提一下离散化,离散化就是把一段很大的区间映射到一个小区间内,这样会节省大量空间,要进行离散化,我们先对端点进行排序,然后去重,然后二分找值就可以了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 #include <cstdio> #include <cstring> #include <cctype> #include <string> #include <set> #include <iostream> #include <stack> #include <cmath> #include <queue> #include <vector> #include <algorithm> #define mem(a,b) memset(a,b,sizeof(a)) #define inf 0x3f3f3f3f #define N 220 #define ll long long using namespace std; #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 struct Seg { double l,r,h; int f; Seg() {} Seg(double a,double b,double c,int d):l(a),r(b),h(c),f(d) {} bool operator < (const Seg &cmp) const { return h<cmp.h; } } e[N]; struct node { int cnt; double len; } t[N<<2]; double X[N]; void pushdown(int l,int r,int rt) { if(t[rt].cnt)//当前的边被标记,就把当前的长度加上 t[rt].len=X[r+1]-X[l]; else if(l==r)//当为一个点的时候长度为0 t[rt].len=0; else//其他情况把左右两个区间的值加上 t[rt].len=t[rt<<1].len+t[rt<<1|1].len; } void update(int L,int R,int l,int r,int rt,int val) { if(L<=l&&r<=R) { t[rt].cnt+=val;//加上标记的值 pushdown(l,r,rt);//像下更新节点 return; } int m=(l+r)>>1; if(L<=m) update(L,R,lson,val); if(R>m) update(L,R,rson,val); pushdown(l,r,rt); } int main() { int n,q=1; double a,b,c,d; while(~scanf("%d",&n)&&n) { mem(t,0); int num=0; for(int i=0; i<n; i++) { scanf("%lf%lf%lf%lf",&a,&b,&c,&d); X[num]=a; e[num++]=Seg(a,c,b,1);//矩形下面用1来标记吗 X[num]=c; e[num++]=Seg(a,c,d,-1);//上面用-1来标记 } sort(X,X+num);//用于离散化 sort(e,e+num);//把矩形的边的纵坐标从小到大排序 int m=unique(X,X+num)-X; double ans=0; for(int i=0; i<num; i++) { int l=lower_bound(X,X+m,e[i].l)-X;//找出离散化以后的值 int r=lower_bound(X,X+m,e[i].r)-X-1; update(l,r,0,m,1,e[i].f); ans+=t[1].len*(e[i+1].h-e[i].h); } printf("Test case #%d\nTotal explored area: %.2lf\n\n",q++,ans); } return 0; }